今回から、ボケとパンフォーカスのシリーズです。
パンフォーカス(pan focus)とは、近くから遠くまでの全てにピントが合っていること。ボケとは正反対のようですが、意外と関係があったりするのです。
ボケた写真でも、離れてみるとボケとはわからなくなる場合があります。それは、ボケが小さくなりすぎて認識できなくなるからです。
どれくらい小さいとボケと認識できなくなるか、実はこの大きさについて2つの考え方(値)があるのです。
関連 トピックス一覧
許容錯乱円の大きさに2つの考え方:ボケとパンフォーカス(1)
ピントが合っているように見える範囲・被写界深度:ボケとパンフォーカス(2)
被写界深度を計算してみた:ボケとパンフォーカス(3)
花と人と星にピントが合って見える:ボケとパンフォーカス(4)
過焦点距離を使って撮影してみました:ボケとパンフォーカス(5)
絞りすぎてボケた・回折現象に注意:ボケとパンフォーカス(6)
ボケと錯乱円
点光源の被写体を撮影した場合、ピントが合っていれば、下図の赤い線のようにイメージセンサー上では点として写ります。
一方、ピントがずれた場合には、青い線のように、オレンジ色で示したぼやけた丸い円として写ります。

この円を錯乱円(さくらんえん)といいます。ピントがずれるほど、大きな円として写ります。
英語では "circle of confusion" ですが、"錯乱"とはわかりにくいですね。絞り開放ながら写る:玉ボケのゴミはどこから?では玉ボケと紹介しましたが、意味的には、"ボケ円"でしょうか。
許容錯乱円
ボケている錯乱円が小さくなっていくと、出力した時に、もはやボケとは識別できなくなります。この最小錯乱円のことを許容錯乱円といいます。
許容錯乱円(permissible circle of confusion):ボケとして識別できない最小の錯乱円
より詳しくは、出力した写真やディスプレイなどでボケとして識別できない、イメージセンサー上の最小の錯乱円、になります。
許容錯乱円の大きさに2つの考え方
許容錯乱円は、あくまでもイメージセンサー(フィルム)上で想定する円です。
一方、どの程度の大きさがボケとして識別できないのか、その大きさを決めるのは、出力した写真やディスプレイなどでの、許容錯乱円を拡大した円のサイズになります。
最終的に、拡大率(出力した写真とイメージセンサーの大きさの比)から、イメージセンサー上での大きさを許容錯乱円のサイズとします。
そして、許容錯乱円のサイズについては、次の2つの考え方(値)があります。
1)肉眼で鑑賞する場合:31.4μ
印刷して写真展などで鑑賞する場合です。フィルム時代からある考え方で、フルサイズ(35mmフィルム)のイメージセンサー上の場合、参考1)では、許容錯乱円の大きさは31.4μとされています。
約30μと丸めてもいいのですが、円周率の10倍の数字と思えば、覚えやすいかも(笑)。
この場合、鑑賞する写真のサイズ、写真までの距離、見る人の視力などによって、ボケの識別具合が異なるので、許容錯乱円の大きさは変化します。一方、撮影する機材の影響は受けません。
31.4μとする根拠ですが、参考1)によると、展示されたポストカードサイズ(対角長180mm)の写真を鑑賞する時の目と写真の間の距離(450mm)において視力1.0の人が識別できる2点間の最小距離は、フルサイズのイメージセンサー(35mmフィルム)上では、31.4μ とされています。
なお、フルサイズのイメージセンサーの対角長を43.3mmとしていますが、デジタルカメラの機種によって、微妙に異なります。私のSONY α7RIIでは、35.9mm☓24.0mmなので、対角長は43.2mmとなります。許容錯乱円は31.4μのままです。
許容錯乱円31.4μは、視力1.0の基準が根拠
この許容錯乱円の大きさ、実は、視力1.0の基準が根拠になっているようです。
そして、もう一つの仮定は、ポストカードサイズ(対角長180mm)と写真までの距離を 450mmとしていることです。180mmと450mmという長さよりも、この比(2.5倍)が関係します。下の、許容錯乱円の計算式で説明しています。
視力1.0の基準は、視角1分(60分の1゜)のすき間を識別できることです。具体的には、
5mの距離から、ランドルト環のすき間が識別できるかを判定します。ランドルト環のすき間は、日本の規格で1.5mm、正確には国際規格(ISO)の1.4544・・mmです。
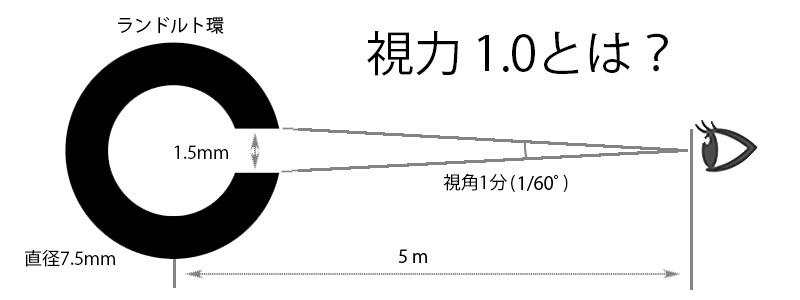
視力1.0とは、5mの距離から1.5mmのすき間が識別できること。これが半分の2.5mだと視力は0.5に、倍の10mだと2.0になります。
そして、視力1.0で、ポストカードサイズの写真上で識別できる2点間の最小距離は、視角1分の関係と写真までの距離(450mm)から、tan(1/60) × 450 × 1000 = 131μとなります。
また、印刷(拡大)前のイメージセンサー上では、拡大率、つまりポストカードとフルサイズセンサーの対角長の比(180/43.3)で割って、31.4μとなります。
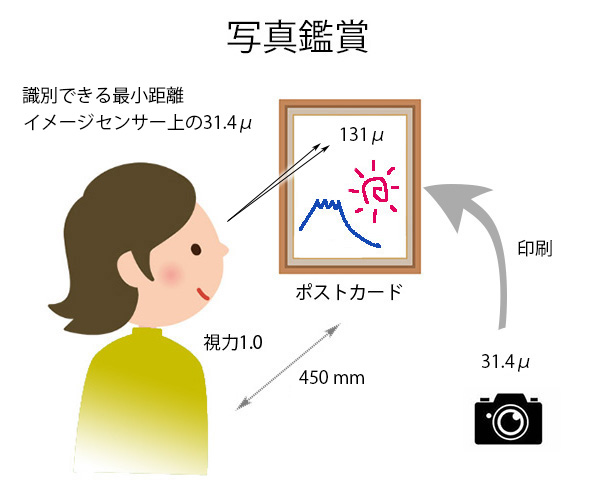
写真鑑賞の場合、許容錯乱円に関係するのは、視力と、写真の大きさと写真までの距離の比です。
許容錯乱円の計算式
より簡便に計算するために、フルサイズでの許容錯乱円の計算式を考えてみました。あらかじめ決めているのは視力が1.0という点だけです。
写真までの距離(mm)と写真の対角長の比が関係する点がポイントですね。許容錯乱円(μ)は、その比の12.6倍になります。
逆に、標準的な基準(31.4μ)でボケているかどうかを判断したいのなら、写真の対角長の2.5倍は離れてみましょう、ということになります。先に示したように、ポストカード(対角長180mm)なら450mmですね。4つ切りサイズ(対角長396.9mm)なら、約1m(99.2cm)です。
ブログで見る場合の許容錯乱円:14.5μ
実際に、はてなブログで見る場合の許容錯乱円の大きさを計算してみましょう。
上の式で、
写真までの距離:45cm
写真の対角長:39cm
(22インチディスプレイで、私のブログの写真を拡大表示したサイズ)
から計算すると14.5μ (約15μ) になります。
画像を、ポストカードサイズより拡大しているので、許容錯乱円は小さくなっています。
2)画像拡大する場合:α7RIIでは4.5μ
もうひとつの考え方は、工業的な画像処理や、写真の現像や画像処理などで、画像を拡大して見る場合です。こちらは、最小単位である画素サイズでのボケの判断になります。
この場合、写真のサイズや見る距離、視力などの影響は受けません。一方、画素(1ピクセル)の大きさは撮影機材で変化します。
画像を拡大するということは、上の許容錯乱円の計算式で説明した、写真までの距離(mm)と写真の対角長の比がかなり小さくなる場合ですね。
具体的には、イメージセンサーの画素ピッチ(画素間隔)又はエアリーディスク径のどちらか大きい方の値になるとされています2)。ただし、エアリーディスク径にはレンズの収差が関係するとされ、レンズによっても異なってきます3)。
例えば、SONY α7RIIでは、イメージセンサーの画素サイズ(センサーサイズ/記録画素数)は縦横とも 4.5μ になります。
センサーサイズ:35.9mm ☓ 24.0mm
記録画素数(最大):7952 ☓ 5304
画素サイズ(横、縦):4.51μ、4.52μ
ただし、工業的に製品検査などに使う場合を除き、通常は、ピクセル単位まで拡大することはありませんね。

デジタル的にいくらでも画像を拡大できる場合、ピクセル単位(画素サイズ)で判別できるようになります。
どちらを使うか
許容錯乱円の大きさとして、2つの考え方(値)があることがわかりました。いったいどちらを使えばいいのでしょうか。
それは、許容錯乱円から何をしたいかによって決まります。
そもそも許容錯乱円はイメージセンサー上で想定(仮定)するものにすぎず、その大きさ自体を問題にすることはありません。
このシリーズでは、風景や花などの写真を撮る場合を想定して、許容錯乱円から、ピントが合っているように見える範囲(被写界深度)を求めたりしていくので、今後は、31.4μ(丸める場合は30μ)の方を使っていきます。
もちろん、写真やディスプレイの大きさや距離、視力などによって異なります。デジタル拡大できることを考えると、許容錯乱円は、31.4μより小さくなる傾向です。
例えば、参考4)のスーパハイビジョン(8K)カメラの例では、許容錯乱円直径は、画素サイズの2倍(フルサイズで 9.8μ )としています。根拠は不明ですが、大画面で拡大してみることを想定しているのでしょうか。
参考
1)デジタルカメラの手ぶれ補正効果に関する測定方法および表記方法(pdf) p.36
世界で最もポピュラーなポストカードサイズの写真を鑑賞する際、目と写真の間の平均的な距離は 450mm 程度とされている。この場合、視力 1.0 の人が判別できる 2 点 間の最小距離[μm]は、
tan(1/60)×450×1000/4.16 = 31.4
である。ここで 4.16 は、ポストカードサイズと 35mm フィルム 1 コマの対角長の比(180/43.3)である。
2)知っておきたい撮影レンズの基礎(東芝、pdf)
4) スーパーハイビジョンの撮像技術の研究開発動向(NHK、pdf)
あとがき
ボケているかどうかは、写真やディスプレイの大きさや距離、視力などによって異なります。許容錯乱円、絶対的な値ではなく、心理的物理量なんでしょう。全体的な流れとしては、小さくなっていく感じで、画素サイズに近づいています。
カメラの性能があがり撮影画素数が大きくなると画素サイズが小さくなり、また、スマホなどで自由にズームできるようになると、わずかなピンぼけでもわかりやすくなるので注意ですね。私のように、ほとんどがボケた写真なら、問題ないですが(笑)。