レンズを前に出すと、より大きく写せることを紹介しました。しかし、前に繰り出すとはいっても、限界がありますね。
この場合、レンズを前後逆にして使うことにより、撮影倍率をさらに大きくすることが可能な場合があります。 今回は、35mmレンズ( Ai Nikkor 35mm F1.4S)を例に、そのメカニズムなどに迫ってみます。
関連
レンズを逆にして超マクロ:レンズの基礎(4)
リバース・マクロとは
レンズを前後逆にして使うことにより、撮影倍率をかなり大きくすることが可能です。特に、広角系のレンズ(レトロフォーカスレンズ)を逆にして使うと、一般的には等倍以上、レンズによっては2倍以上に高めることが可能です。
マクロレンズよりも、大きな写真が撮れます。私のマクロ( SONY FE 90mm F2.8 Macro G OSS )の撮影倍率は等倍ですが、今回は、この2倍程度の倍率になります。
欠点は、ピントの合う範囲が限定されることと、近づきすぎて暗くなることでしょうか。
使えるレンズは
長い焦点距離のレンズではイメージセンサーに像を結ぶことができなくなるため、広角〜標準域のレンズが適し、広角レンズの方が撮影倍率が大きくなります。
特に、広角系は以前紹介したように、レトロフォーカスといって、レンズの後ろに主点があるので、逆にするとレンズの前に主点がくることになります。なので、大きく繰り出すことになっても、レンズは撮影範囲に収まります。
ピント合わせ
レンズを大きく繰り出すので、撮影距離が限定されます。無限遠にも合いません。カメラ自体を前後させてピントを合わせます。
フォーカスリングは機能しないとするサイトもありますが、機能していないのではなく、回しても撮影距離はほとんど変化しないだけです。
撮影倍率


ちなみに、マクロレンズ( SONY FE 90mm F2.8 Macro G OSS )に、さらに25mmの接写リングををつけた場合の最短距離での撮影倍率は、約1.6倍でした。
リバースの光路図
実際のレンズ全体を1枚の凸レンズになると仮定して、リバースにした場合の光路図を図示してみました。
レトロフォーカスレンズなので、前後を逆にすると、主点はレンズの前にきます。マウントアダプターなどの長さを加えると、主点はずいぶん前の方に繰り出すことになります。
実測値として、撮影倍率()を1.8倍、イメージセンサーから被写体までの距離(撮影距離:a+b)を180mmを使用します。
以上より、a=64mm、b=116mmとなります。レンズの公式により、この場合の焦点距離は、f=41.3mmとなり、表示焦点距離の35mmより長くなります。また、レンズ繰り出し量(x=b-f)は、74.4mmとかなり大きいことなります。
また、フランジバック18mm、マウントアダプター28mm、リバースリング4mm、レンズ群の長さ62mmを合計すると、マウント面までは112mmとなります。実際はマウント面より、7mmほどレンズがでています。
よって、全体として以下のようになります。レンズは大きく繰り出された状態なので、ピントリングを回しても、撮影範囲にはほとんど変化がありません。
なお、下図では、小数点以下を四捨五入して表示しているので、合計が一致しない場合があります。
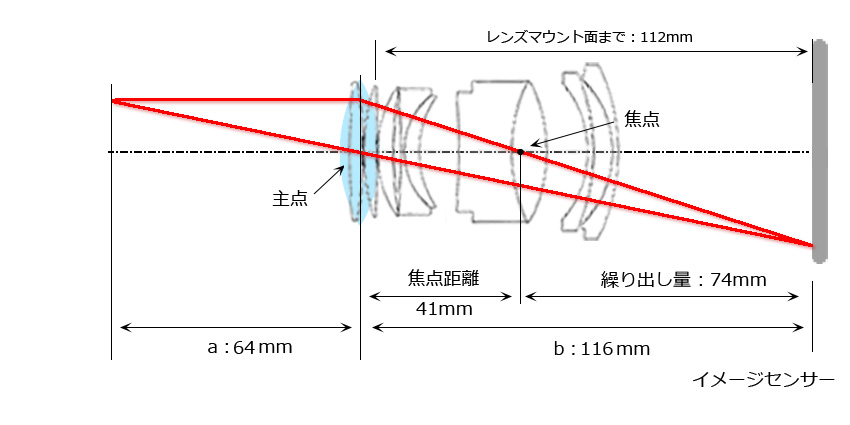
レンズを前後逆につけた場合の光路図:主点に一枚の凸レンズがあるイメージです。繰り出し量は大きいのですが、レトロフォーカスレンズでは、レンズ群の前方に主点がくるので、大きく繰り出しても、レンズ全体は撮影距離内に収まります。
通常の光路図
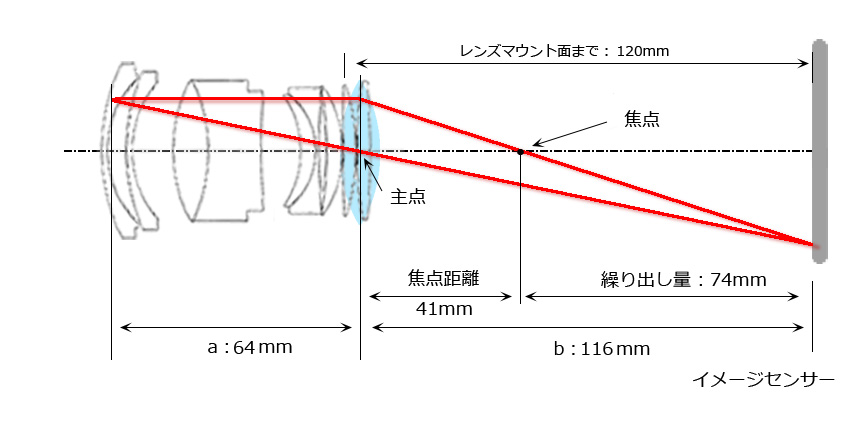
レンズを前後逆にしない通常の場合で、撮影倍率が1.8倍になる光路図を考えてみます。上で求めた焦点距離(41.3mm)と繰り出し量(74.4mm)を使うので、上と同じ光路図になります。また、フランジバック18mm、マウントアダプター28mm、繰り出し量74mmを合計すると、マウント面までは120mmとなります。
1枚の凸レンズと仮定しているので、レンズを前後にしても変化がないわけです。ただし、主点がレンズの後ろにあるので、レンズ全体は撮影距離を超えて飛び出すことになり、実際の撮影は無理ですね。
繰り出し量と撮影距離
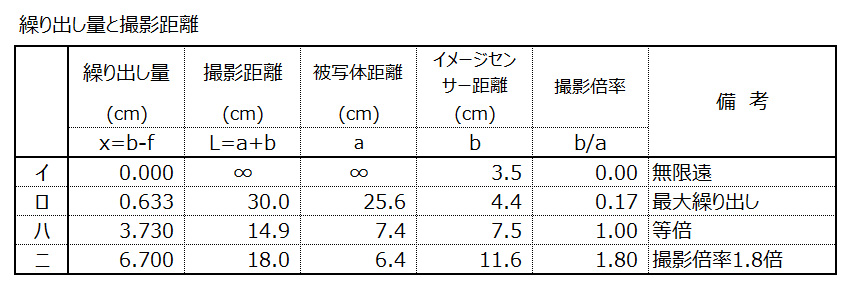
前回と同じように、繰り出し量と撮影距離(撮影できる範囲)の関係を下の表とグラフに示します。通常の場合を想定していますが、1枚の凸レンズと仮定しているので、レンズを逆にした場合も同じです。
1)イは、無限遠の場合で、イメージセンサー距離は表示焦点距離となります。
2)ロは、最大に繰り出した場合です。
3)ハは、撮影倍率が等倍になるように繰り出した場合です。等倍で、撮影距離は最小になります。
4)ニは、撮影倍率が1.8倍になるように繰り出した場合です。
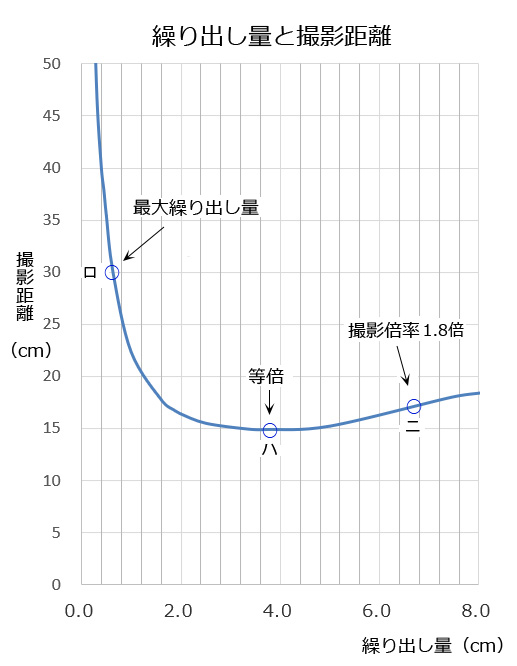
下のグラフから分かるように、レンズの繰り出し量が2cm以上では、繰り出し量を大きくすると撮影倍率は上がりますが、撮影できる範囲である撮影距離はほとんど変化がありません。これが、フォーカスリングが無効に感じる理由です。
最後に
レンズを逆につける方法、マクロレンズを買わなくても超マクロ撮影ができるので、フィルムカメラ時代から利用されていたようです。しかし、どうして、大きく写せるのか、また、ピントリングが効きにくくなるのか、うまく説明したサイトは見つかりませんでした。。。
なお、今回の計算とか光路図は、私の推測なので間違っているかもしれませんので、ご了解を。